Este dibujo en 3D, al ponerlo en vista isométrica, resulta esta vista que parece imposible de realizar.
jueves, 28 de abril de 2011
viernes, 15 de abril de 2011
LOCOMOTORA
Aquí tenéis una locomotora que dibuje en su día. a ver si os gusta.
Una segunda versión con las mismas ruedas.
DIBUJAR CURVAS CON EXCEL
Vamos a intentar explicar cómo dibujar curvas en Solid Edge ayudándonos de Excel.
Para ello debemos conocer la ecuación matemática de la curva.
Naturalmente cuanto más complicada sea esta ecuación más complicado será encontrar como trasladar esta ecuación a Excel.
Como no pretendo dar una clase de matemáticas, para este tutorial utilizaré una curva, la parábola, que a la vez que tiene una ecuación fácil, es posible que alguna vez tengamos que dibujarla.
La necesitaremos si queremos dibujar la pantalla de una antena parabólica, las letras de McDonals o el faro de un coche antiguo, entre otras cosas.
La parábola es una curva en la que todos sus puntos equidistan (misma distancia) de un punto fijo llamado “Foco” y de una recta fija llamada “Directriz”.
Si A es un punto de la parábola tenemos:
AF = AD
La distancia fija entre el foco y la directriz se llama “Parámetro” y lo designaremos como P.
Para tener una ecuación más fácil haremos que el vértice de la parábola sea el origen de coordenadas y que la directriz sea vertical.
Una vez dibujada siempre podremos girarla y trasladarla si es necesario.
En estas condiciones la ecuación matemática de la parábola es:
Despejando la y tendríamos:
Una particularidad importante de la parábola es que todos los rayos horizontales que lleguen a la parábola se reflejarán pasando por el foco.
En esto se basan las antenas parabólicas, colocan el receptor en el foco y así captan todas las señales que llegan a la pantalla en dirección horizontal.
En los coches antiguos hacían el faro de forma parabólica y colocaban la bombilla en el foco, así los haces de luz que emitía la bombilla se reflejaban de forma horizontal.
Bien después de estas curiosidades, vamos ya a dibujar una parábola.
Fijándonos en la ecuación de la parábola vemos que para cada valor del parámetro P tendremos una curva diferente.
Pongamos un ejemplo:
Queremos dibujar una parábola que tenga como parámetro 100.
Su ecuación será :
Bastará ir dando valores a x y obtener su correspondiente y
Y así puntos y más puntos, cuantos más puntos y más cercanos estén más perfecta nos saldrá la parábola.
Dibujamos todos nuestros puntos en un boceto, hacemos una spline que pase por todos estos puntos y listo.
Tarea aburrida y fácil de cometer errores, vamos a hacer que Excel haga esta tarea por nosotros y con la seguridad de que no habrá errores.
Cuando, en Solid Edge, relacionemos este con Excel entenderá que en la columna A están las coordenadas de las x, en la columna B las coordenadas de las y en la columna C las coordenadas de las z (si la curva fuera de tres dimensiones, no es el caso de la parábola que es una curva plana).
En el resto de columnas podremos poner los datos que queramos para ayudarnos a calcular nuestros puntos.
Veamos cómo preparar una tabla Excel para la parábola.
Siempre fuera de las columnas A, B y C como hemos dicho antes, colocamos en una celda (yo he escogido la G1) un valor, que yo he llamado PRECISION, y que nos servirá para tener más o menos puntos al ir sumando a las x este valor.
En otra celda, la G3, he colocado el valor del parámetro que es lo que nos determina la forma de la parábola, así simplemente cambiando este valor tendremos calculados todos los puntos de nuestra curva.
Ahora tenemos que poner nuestra ecuación en las columnas A, B y C
En la A las x, empezamos en A1 con el cero y en la celda siguiente (A2) que nos coja la anterior (A1) más la precisión G1. Notar que hemos puesto signo $ (dólar) delante de la G y del 1 para que luego al arrastrar para tener más puntos no arrastre los índices y siempre coja G1.
En la columna B las y que nos las dará la ecuación de la curva, si recordamos que era:
en Excel la P la tenemos en G3 y las x en A1, por lo tanto nuestra ecuación en Excel será:
= RAIZ(2*$G$3*A1), igual que antes delante de la G y delante del 3 hemos puesto el signo $ (dólar) para que siempre coja el valor de la G3.
En la columna C colocaríamos las coordenadas de las z pero como esta curva es plana todo deben ser ceros, en C1 ponemos 0 y en la siguiente (C2) hacemos que copie la C1 con signos $ (dólar) para que siempre sea 0.
Solo nos falta seleccionar las celdas A2, B2 y C2 y arrastrar hacia abajo todo lo que queramos para tener más puntos.
Guardamos nuestra tabla y ya podemos ir a Solid Edge para ver como dibujar nuestra curva.
Vamos a Solid Edge y abrimos una pieza nueva.
Vamos a la pestaña “Superficies” y desplegamos el cuadro “Puntos significativos” para elegir “Curva según tabla”.
Nos sale una pantalla “Insertar objeto”.
Marcamos la opción “Crear desde archivo”.
Damos a “Examinar”, buscamos nuestro fichero Excel y lo abrimos.
De vuelta a la pantalla “Insertar Objeto” damos a “Aceptar” y nos dibujará en planta la curva.
sábado, 22 de enero de 2011
lunes, 10 de enero de 2011
miércoles, 5 de enero de 2011
martes, 4 de enero de 2011
ENGRANAJES CONICOS CON Solid Edge
En general, los engranajes cónicos se suelen emplear para ejes que se cortan a 90º; sin embargo pueden fabricarse también para un ángulo cualquiera.
Aquí mostraremos como dibujar los engranajes para ejes a 90º.
Las medidas de los engranajes cónicos de dientes rectos se calculan en función del módulo, el numero de dientes y el ángulo de posición de los ejes.
Un par de engranajes cónicos han de calcularse conjuntamente, formando pareja ya que el semiángulo de los conos primitivos han de complementarse, es decir sumar 90º, por esta razón no pueden intercambiarse con otros engranajes de distinto número de dientes que los calculados.
Los dientes se definen sobra la base mayor del cono primitivo.
Cuando se proyectan sobre el perfil complementario, tienen la misma forma que la de un engranaje cilíndrico de dientes rectos que tiene un radio primitivo igual a la generatriz del cono complementario.
Después de esta introducción sobre los engranajes cónicos, vamos a pasar a dibujar el piñón de un par de engranajes con estos datos.
Módulo = m = 1
Nº de dientes del piñón = z = 16
Nº de dientes de la rueda = Z = 32
Con estos datos calculamos:
Diámetro primitivo del piñón = m * z = 16 mm.
Diámetro primitivo de la rueda = m * Z = 32 mm.
En lugar de utilizar fórmulas matemáticas, no siempre fáciles de asimilar, vamos a dibujar un boceto auxiliar que acotándolo de forma adecuada nos de los datos que necesitamos para el dibujo de los dientes.
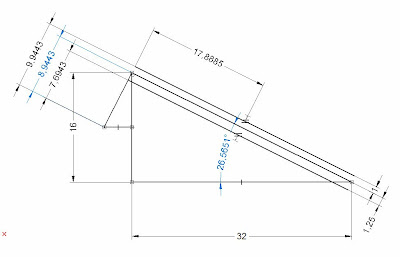
En un plano cualquiera dibujamos una línea horizontal de longitud 32 ( diámetro primitivo de la rueda) y otra vertical de longitud 16 (diámetro primitivo del piñón), unimos los extremos para formar un triángulo.
Acotamos el ángulo y guardamos el valor para utilizarlo luego ( A = 26'5651).
Dibujamos una linea horizontal por el punto medio de la línea de longitud 16 y una línea perpendicular a la línea inclinada del triángulo.
Hacemos que corten.
El addendum del diente (distancia entre el diámetro primitivo y el diámetro exterior) se hace generalmente igual al módulo (en este ejemplo a = 1 mm.).
El dedendum del diente (distancia entre el diámetro primitivo y el diámetro del fondo) se hace generalmente igual al módulo multiplicado por 1'25 ( en este ejemplo b = 1'25 mm.).
Dibujamos una paralela, hacia afuera, a la línea inclinada del triángulo y distancia a = 1.
Dibujamos otra paralela, hacia adentro, a una distancia b = 1'25.
Acotando lo que se indica en la imagen obtenemos:
Datos para el perfil "complementario"
Radio exterior = 9'9443 mm. (diámetro 19'8886)
Radio primitivo = 8'9443 mm. (diámetro 17'8886)
Radio de fondo = 7'6943 mm. (diámetro 15'3886)
Como, normalmente, el ángulo de presión es de 20º, el radio de la circunferencia de base será:
g = radio primitivo * coseno 20º = 8'9443 * cos 20º = 8'4049
Este es el valor que debemos poner en la hoja de cálculo Excel.
Con estos datos y lo explicado en el tutorial de dibujo de engranajes cilíndricos (también publicado en este blog) ya podemos dibujar el hueco del diente para el perfil complementario.
El número de dientes ideal de este perfil complementario, será:
y el ángulo
Ahora vamos a dibujar el perfil del cuerpo del engranaje en el plano ALZADO (ya que el hueco del diente se nos ha dibujado en PLANTA).
Para ello utilizaremos una protrusión por revolución.
Dibujamos una recta horizontal que pase por el origen y tenga 8'9443 mm. de longitud (radio primitivo del perfil complementario).
Por el final de esta otra linea vertical y finalmente otra para completar un triángulo.
Acotamos el ángulo y modificamos su valor a 26'5661, que es el valor del ángulo A que habíamos obtenido al principio y que dijimos que había que guardar.
La línea inclinada del triángulo será el eje de revolución.
Aquí mostraremos como dibujar los engranajes para ejes a 90º.
Las medidas de los engranajes cónicos de dientes rectos se calculan en función del módulo, el numero de dientes y el ángulo de posición de los ejes.
Un par de engranajes cónicos han de calcularse conjuntamente, formando pareja ya que el semiángulo de los conos primitivos han de complementarse, es decir sumar 90º, por esta razón no pueden intercambiarse con otros engranajes de distinto número de dientes que los calculados.
Los dientes se definen sobra la base mayor del cono primitivo.
Cuando se proyectan sobre el perfil complementario, tienen la misma forma que la de un engranaje cilíndrico de dientes rectos que tiene un radio primitivo igual a la generatriz del cono complementario.
Después de esta introducción sobre los engranajes cónicos, vamos a pasar a dibujar el piñón de un par de engranajes con estos datos.
Módulo = m = 1
Nº de dientes del piñón = z = 16
Nº de dientes de la rueda = Z = 32
Con estos datos calculamos:
Diámetro primitivo del piñón = m * z = 16 mm.
Diámetro primitivo de la rueda = m * Z = 32 mm.
En lugar de utilizar fórmulas matemáticas, no siempre fáciles de asimilar, vamos a dibujar un boceto auxiliar que acotándolo de forma adecuada nos de los datos que necesitamos para el dibujo de los dientes.
En un plano cualquiera dibujamos una línea horizontal de longitud 32 ( diámetro primitivo de la rueda) y otra vertical de longitud 16 (diámetro primitivo del piñón), unimos los extremos para formar un triángulo.
Acotamos el ángulo y guardamos el valor para utilizarlo luego ( A = 26'5651).
Dibujamos una linea horizontal por el punto medio de la línea de longitud 16 y una línea perpendicular a la línea inclinada del triángulo.
Hacemos que corten.
El addendum del diente (distancia entre el diámetro primitivo y el diámetro exterior) se hace generalmente igual al módulo (en este ejemplo a = 1 mm.).
El dedendum del diente (distancia entre el diámetro primitivo y el diámetro del fondo) se hace generalmente igual al módulo multiplicado por 1'25 ( en este ejemplo b = 1'25 mm.).
Dibujamos una paralela, hacia afuera, a la línea inclinada del triángulo y distancia a = 1.
Dibujamos otra paralela, hacia adentro, a una distancia b = 1'25.
Acotando lo que se indica en la imagen obtenemos:
Datos para el perfil "complementario"
Radio exterior = 9'9443 mm. (diámetro 19'8886)
Radio primitivo = 8'9443 mm. (diámetro 17'8886)
Radio de fondo = 7'6943 mm. (diámetro 15'3886)
Como, normalmente, el ángulo de presión es de 20º, el radio de la circunferencia de base será:
g = radio primitivo * coseno 20º = 8'9443 * cos 20º = 8'4049
Este es el valor que debemos poner en la hoja de cálculo Excel.
Con estos datos y lo explicado en el tutorial de dibujo de engranajes cilíndricos (también publicado en este blog) ya podemos dibujar el hueco del diente para el perfil complementario.
El número de dientes ideal de este perfil complementario, será:
y el ángulo
Ahora vamos a dibujar el perfil del cuerpo del engranaje en el plano ALZADO (ya que el hueco del diente se nos ha dibujado en PLANTA).
Para ello utilizaremos una protrusión por revolución.
Dibujamos una recta horizontal que pase por el origen y tenga 8'9443 mm. de longitud (radio primitivo del perfil complementario).
Por el final de esta otra linea vertical y finalmente otra para completar un triángulo.
Acotamos el ángulo y modificamos su valor a 26'5661, que es el valor del ángulo A que habíamos obtenido al principio y que dijimos que había que guardar.
La línea inclinada del triángulo será el eje de revolución.
A partir del punto B, trazamos una linea horizontal de longitud 1mm. (altura de la cabeza del diente "addendum") y unimos el final de ésta con el punto A.
El resto de medidas del perfil de este cuerpo, hasta completar la zona rayada, según nuestro diseño.
Nótese de obligatoria mente las líneas "1" y "2" deben ser perpendiculares al eje de rotación.
Salvo las lineas que forman el perfil, el resto las hacemos de construcción.
Dibujamos un punto en A.
Salimos del boceto y hacemos la protrusión por revolución con este boceto.
Para hacer el hueco del diente utilizaremos la operación "Cortar por secciones".
Nos aseguramos de que esté la opción "Seleccionar = Cadena" y marcamos el perfil del diente.
Cambiamos la opción Seleccionar a "Punto" y marcamos el punto que hemos dibujado en A.
Muestra y terminar.
Redondeamos las aristas del fondo y de la cresta del diente con un radio igual al módulo dividido por 6.
En este ejemplo será radio = 0'17.
Para finalizar haremos un patrón circular.
Seleccionar operaciones: Vaciado y redondeo, aceptar.
Seleccionar plano.
Seleccionar centro del circulo, arrastramos para crear un circulo cualquiera, movemos el ratón para seleccionar un lado (no importa cual).
Escribimos número de copias, aquí serán 16.
Aceptar y listo.
Agujero para eje, chavetero y demás a gusto del consumidor.
lunes, 3 de enero de 2011
Suscribirse a:
Comentarios (Atom)